1. Số hữu tỉ
Ở lớp 6 ta đã biết: những phân số đều bằng nhau là những cách viết khác nhau của và một số. Ta hotline số chính là số hữu tỉ.
Bạn đang xem: Tập hợp số q
Nhắc lại: Để viết được những phân số mới bởi phân số vẫn cho, ta có các phương pháp: Nhân cả tử và mẫu với cùng một trong những khác 0; phân tách cả tử cùng mẫu cho một mong chung; đổi dấu cả tử và chủng loại của phân số ban đầu.
Ví dụ:
+)(3=dfrac31=dfrac62=dfrac-9-3=...)
+)(-0,25=dfrac-14=dfrac1-4=dfrac-28=...)
+)(3dfrac12=dfrac72=dfrac144=dfrac-21-6=...)
+)(0=dfrac01=dfrac0-2=dfrac04=...)
Như vậy, những số(3);(-0,25);(3dfrac12);(0)đều là những số hữu tỉ.
Định nghĩa: Số hữu tỉ là số viết được bên dưới dạng phân số(dfracab)với(a,bin Z;b e0).
Kí hiệu: Tập hợp các số hữu tỉ được kí hiệu là(Q).
Ví dụ:
+)(0,123=dfrac1231000)nên(0,123)là một số trong những hữu tỉ.
+) Xét số nguyên(a). Ta có(a=dfraca1)nên(a)cũng là một số hữu tỉ.
Nhận xét: Mỗi số nguyên là một trong những hữu tỉ. Vày đó, hiển nhiên ta có: mỗi số thoải mái và tự nhiên cũng là một vài hữu tỉ.
(Nsubset Zsubset Q)

54002
2. Màn trình diễn số hữu tỉ trên trục số
Ở các lớp dưới, ta đã màn biểu diễn được các số tự nhiên và thoải mái và số nguyên trên trục số. Bây giờ, ta tiếp tục biểu diễn các số hữu tỉ.
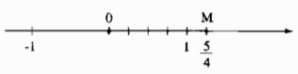
Ví dụ 1: màn biểu diễn số(dfrac54)trên trục số.
Các bướclàm:
- phân chia đoạn thẳng đơn vị (chẳng hạn đoạn trường đoản cú điểm 0 tới điểm 1)thành 4 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng(dfrac14)đơn vị cũ.
- Số hữu tỉ(dfrac54)được màn trình diễn bởi điểm(M)nằm bên nên điểm0và bí quyết điểm 0 một đoạn bằng 5 đơn vị mới.
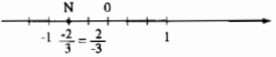
Ví dụ 2: biểu diễn số(dfrac2-3)trên trục số.
Các bước làm:
- Viết số hữu tỉ đã cho về dạng phân số tất cả mẫu số dương:(dfrac2-3=dfrac-23).
Xem thêm: Cách Quay Video Đẹp Bằng Iphone, Mẹo Biến Iphone Thành Máy Quay Phim Chuyên Nghiệp
- phân tách đoạn thẳng đơn vị thành 3 phần bởi nhau, mang một đoạn làm đơn vị mới thì đơn vị chức năng mới bằng(dfrac13)đơn vị cũ.
- Số hữu tỉ(dfrac-23)được màn biểu diễn bởi điểm(N)nằm bên trái điểm 0 và phương pháp điểm 0 một đoạn bởi 2 đơn vị mới.
Chú ý: Điểm màn trình diễn số hữu tỉ(x)được gọi là điểm(x).
3. đối chiếu hai số hữu tỉ
+) Với hai số hữu tỉ(x,y)bất kì, ta luôn có:hoặc(x=y),hoặc(x>y), hoặc(x.
+) Để đối chiếu hai số hữu tỉ (x,y), ta làm như sau:
Viết nhì số(x,y)dưới dạng hai phân số gồm cùng mẫu dương:(x=dfracam;y=dfracbmleft(m>0 ight)).So sánh nhị tử số:(a>bRightarrow x>y)
(a
(a=bRightarrow x=y)
Ví dụ 1: so sánh hai số hữu tỉ(-0,75)và(dfrac-12).
Lời giải:
Ta có:(-0,75=dfrac-75100=dfrac-34;dfrac-12=dfrac-24).
Do(-3.
Ví dụ 2: So sánh nhì số hữu tỉ(2dfrac13)và 0.
Lời giải:
Ta có(2dfrac13=dfrac73;0=dfrac03).
Do(7>0Rightarrowdfrac73>dfrac03Rightarrow2dfrac13>0).
Chú ý: Tương từ bỏ như số nguyên, nếu hai số hữu tỉ(x,y)thỏa mãn(xthì bên trên trục số, điểm(x)nằm phía trái điểm(y).
Như vậy, nhằm so sánh những số hữu tỉ, ta cũng có thể biểu diễn chúng trên và một trục số rồi đưa ra kết luận.
Tính chất: Số hữu tỉ to hơn 0 điện thoại tư vấn là số hữu tỉ dương; Số hữu tỉ nhỏ dại hơn 0 call là số hữu tỉ âm; Số 0 ko là số hữu tỉ dương cùng cũng không là số hữu tỉ âm.














