Xét quy tắc tử T với không khí khuôn là tụ hội \(\Omega \) bao gồm hữu hạn phần tử; những thành phẩm của quy tắc test là đồng tài năng, những trở nên cố đều tương quan cho tới quy tắc test bại.
1. Phép toán bên trên những trở nên cố
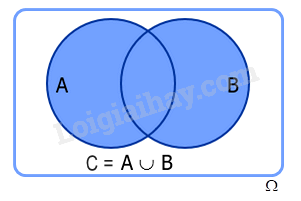
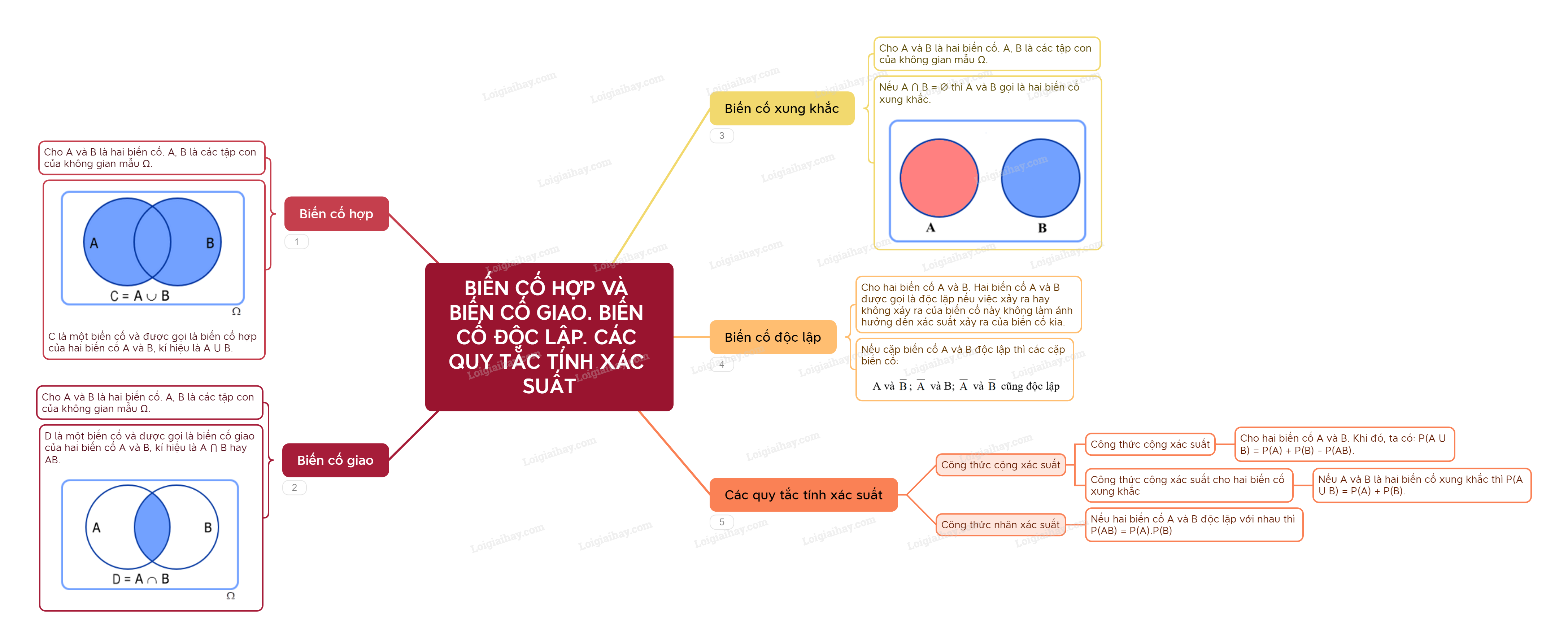
a) Biến cố hợp
Cho nhì trở nên cố A và B. Khi bại A, B là những tập luyện con cái của không khí khuôn \(\Omega \). Đặt \(C = A \cup B\), tao với C là 1 trở nên cố và được gọi là trở nên cố thích hợp của nhì trở nên cố A và B, kí hiệu là \(A \cup B\).
b) Biến cố giao
Cho nhì trở nên cố A và B. Khi bại A, B là những tập luyện con cái của không khí khuôn \(\Omega \). Đặt \(D = A \cap B\), tao với D là 1 trở nên cố và được gọi là trở nên cố gửi gắm của nhì trở nên cố A và B, kí hiệu là \(A \cap B\) hoặc AB.
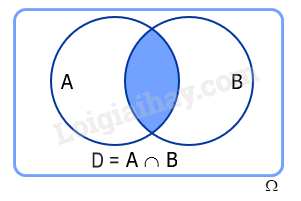
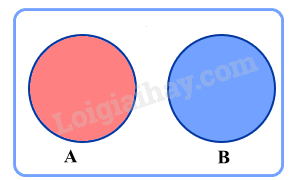
c) Biến cố xung khắc
Cho nhì trở nên cố A và B. Khi bại A, B là những tập luyện con cái của không khí khuôn \(\Omega \). Nếu \(A \cap B = \emptyset \) thì A và B gọi là nhì trở nên cố xung xung khắc.
2. Biến cố độc lập
Cho nhì trở nên cố A và B. Hai trở nên cố A và B được gọi là song lập nếu như việc xẩy ra hay là không xẩy ra của trở nên cố này sẽ không thực hiện tác động cho tới phần trăm xẩy ra của trở nên cố bại.
Chú ý: Nếu A, B là nhì trở nên cố song lập thì từng cặp trở nên cố sau cũng độc lập: A và \(\overline B \); \(\overline A \) và B; \(\overline A \) và \(\overline B \).
3. Các quy tắc tính xác suất
a) Công thức nằm trong xác suất
Cho nhì trở nên cố A và B. Khi bại \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\).
Hệ quả: Nếu nhì trở nên cố A và B là xung xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
b) Công thức nhân xác suất
Cho nhì trở nên cố A và B. Nếu nhì trở nên cố A và B là song lập thì \(P\left( {A \cap B} \right) = P\left( A \right).P\left( B \right)\).
4. Bài tập luyện về Biến cố thích hợp và trở nên cố gửi gắm. Biến cố song lập. Các quy tắc tính xác suất
Bài 1. Gieo nhì con cái xúc xắc bằng vận và đồng hóa học. Xác suất nhằm tổng số chấm bên trên mặt mũi xuất hiện nay của nhì con cái xúc xắc vị 7 là:
A. \(\dfrac{2}{9}\).
B. \(\dfrac{1}{6}\).
C. \(\dfrac{7}{{36}}\).
D. \(\dfrac{5}{{36}}\).
Lời giải: Ta có: \(n(\Omega ) = 6.6 = 36\).
Gọi \(A\):”tổng số chấm bên trên mặt mũi xuất hiện nay của nhì con cái súc sắc vị 7”.
\(A = {\rm{\{ (1;6);(2;5);(3;4);(4;3);(5;2);(6;1)\} }}\).
Do bại \(n(A) = 6\).
Vậy \(P(A) = \dfrac{6}{{36}} = \dfrac{1}{6}\).
Chọn đáp án B
Bài 2. Gieo đồng xu nhì phen tiếp tục. Biến cố \(A\) là trở nên cố “Mặt ngửa xuất hiện nay trúng 1 lần”. Số thành phần của \({\Omega _A}\) là:
A. \(2\)
B. \(1\)
C. \(3\)
D. \(4\)
Lời giải:
Ta có: \({\Omega _A} = \left\{ {NS,SN} \right\}\).
Chọn đáp án A.
Bài 3. Cho quy tắc test với không khí khuôn \(\Omega = \left\{ {1;2;3;4;5;6} \right\}\). Cặp trở nên cố ko đối nhau là:
A. \(A = \left\{ 1 \right\}\) và \(B = \left\{ {2;3;4;5;6} \right\}\)
B. \(C = \left\{ {1;2;5} \right\}\) và \(D = \left\{ {3;4;6} \right\}\)
C. $E = \left\{ {1;4;6} \right\}$ và \(F = \left\{ {2;3} \right\}\)
D. \(G = \Omega \) và \(H = \emptyset \)
Lời giải:
Trong những đáp án tiếp tục mang lại tao thấy chỉ mất đáp án C là ko thỏa mãn nhu cầu ĐK của trở nên cố đối.
Chọn đáp án C.
Bài 4. Có $8$ ngược cân nặng theo lần lượt là $1kg, 2kg, 3kg, 4kg, 5kg, 6kg, 7kg, 8kg$. Chọn tình cờ $3$ ngược cân nặng nhập $8$ ngược cân nặng bại. Tính phần trăm nhằm trọng lượng $3$ ngược cân nặng được lựa chọn ko vượt lên trên quá $9kg$.
A. \(\dfrac{1}{{15}}\)
B. \(\dfrac{1}{7}\)
C. \(\dfrac{1}{{28}}\)
D. \(\dfrac{1}{8}\)
Lời giải: Chọn tình cờ $3$ ngược cân nặng nhập $8$ ngược cân nặng tao với \(\left| \Omega \right| = C_8^3 = 56\)
Gọi $A$ là trở nên cố tuyển chọn được $3$ ngược cân nặng và tổng trọng lượng $3$ ngược cân nặng ko vượt lên trên quá $9 kg$.
Vì
\(\begin{array}{l}1 + 2 + 3 = 6 < 9\\1 + 2 + 4 = 7 < 9\\1 + 2 + 5 = 8 < 9\\1 + 2 + 6 = 9\\1 + 3 + 4 = 8 < 9\\1 + 3 + 5 = 9\\2 + 3 + 4 = 9\end{array}\)
Nên \(\left| A \right| = 7\)
Vậy \(P(A) = \dfrac{{\left| A \right|}}{{\left| \Omega \right|}} = \dfrac{7}{{56}} = \dfrac{1}{8}\)
Chọn đáp án D.
Bài 5. Một cái tàu khoan thăm hỏi dò thám dầu khí bên trên thềm châu lục với phần trăm khoan trúng túi dầu là $0,4$. Xác suất nhằm nhập $5$ phen khoan song lập, cái tàu bại khoan trúng túi dầu tối thiểu một phen.
A. \(0,07776\)
B. \(0,84222\)
C. \(0,15778\)
D. \(0,92224\)
Lời giải:
Gọi A là trở nên cố “chiếc tàu khoan trúng túi dầu”. Ta với \(P\left( A \right) = 0,4\)
Suy đi ra \(\bar A\) là trở nên cố “chiếc tàu khoan ko trúng túi dầu”. Ta với \(P(\bar A) = 0,6\)
Xét quy tắc test “tàu khoan 5 phen độc lập” với trở nên cố
B:“chiếc tàu ko khoan trúng túi dầu phen nào”, tao với \(P(B) = 0,{6^5} = 0,07776\)
Khi bại tao với \(\overline B\) “chiếc tàu khoan trúng túi dầu tối thiểu một lần”. Ta có:
\(P\left( {\overline B} \right) = 1 - P(B) \) \(= 1 - 0,07776 = 0,92224\)
Chọn đáp án D.
Bài 6. Một trạm điều động xe cộ với 15 xe cộ xe hơi nhập bại với 10 xe cộ chất lượng và 5 xe cộ ko chất lượng. Trạm xe cộ điều động tình cờ 4 xe cộ xe hơi cút chở khách hàng, phần trăm nhằm nhập 4 xe cộ xe hơi với tối thiểu 1 xe cộ chất lượng là:
A. \(\frac{{273}}{{1365}}\)
B. \(\frac{{272}}{{273}}\)
C. \(\frac{1}{{273}}\)
D. \(\frac{{1364}}{{1365}}\)
Lời giải:
Số thành phần của không khí khuôn là \(n\left( \Omega \right) = C_{15}^4 = 1365\).
Gọi A là trở nên cố: “trong 4 xe cộ xe hơi với tối thiểu 1 xe cộ tốt” \( \Rightarrow \) Biến cố đối \(\overline A \) “trong 4 xe cộ xe hơi với không tồn tại xe cộ chất lượng nào”.
\( \Rightarrow n\left( {\overline A } \right) = C_5^4 = 5\).
Vậy phần trăm của trở nên cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{5}{{1365}} = \frac{{272}}{{273}}\).
Chọn đáp án B.
Bài 7. Giả sử $A$ và $B$ là nhì trở nên cố nằm trong tương quan cho tới quy tắc test $T$. Khẳng lăm le nào là trong những xác minh sau là đúng?
1) Nếu $A $ và $B$ là nhì trở nên cố song lập thì \(P(A \cup B) = P(A) + P(B)\) .
2) Nếu $A$ và $B$ là nhì trở nên cố xung xung khắc thì \(P(A \cup B) = P(A) + P(B)\) .
3) \(P(AB) = P(A).P(B)\).
A. Chỉ 1 đúng
B. Chỉ 2 đúng
C. Chỉ 3 đúng
D. Cả tía đều sai.
Lời giải:
Dựa nhập lý thuyết trở nên cố đối và trở nên cố song lập tao có:
- Nếu $A$ và $B$ là nhì trở nên cố song lập thì \(P(AB) = P(A).P(B)\) .
- Nếu $A$ và $B$ là nhì trở nên cố xung xung khắc thì \(P(A \cup B) = P(A) + P(B)\).
Vậy chỉ mất $2$ trúng.
Chọn đáp án B.
Bài 8. Xác suất phun trúng đích của một người phun súng là $0,6$. Xác suất nhằm nhập tía phen phun song lập người bại phun trúng đích trúng một phen.
A. \(0,4\)
B. \(0,6\)
C. \(0,096\)
D. \(0,288\)
Lời giải: Gọi A là trở nên cố “người phun súng phun trúng đích”. Ta với \(P\left( A \right) = 0,6\)
Suy đi ra \(\overline A\) là trở nên cố “người phun súng ko phun trúng đích”. Ta với \(P(\overline A) = 0,4\)
Xét quy tắc test “bắn tía phen độc lập” với trở nên cố “người bại phun trúng đích trúng một lần”, tao với những trở nên cố xung xung khắc sau:
• \(B\): “Bắn trúng đích lần thứ nhất và trượt ở nhì phen phun sau”. Ta với \(P(B) = 0,6.0,4.0,4 = 0,096\)
• C: “Bắn trúng đích ở phen phun loại nhì và trượt ở lần thứ nhất và phen loại ba”. Ta có
\(P(C) = 0,4.0,6.0,4 = 0,096\)
• D: “Bắn trúng đích ở phen phun loại tía và trượt ở nhì phen đầu”. Ta có:
\(P(D) = 0,4.0,4.0,6 = 0,096\)
Xác suất nhằm người bại phun trúng đích trúng một phen là:
\(P = P(A) + P(B) + P(C) = 0,096 + 0,096 + 0,096 = 0,288\)
Chọn đáp án D.
Bài 9. Hai cầu thủ đá bóng bớt trị thông thường, từng người được bớt một ngược với phần trăm bàn ứng là $0,8$ và $0,7$. Tính phần trăm nhằm chỉ mất $1$ cầu thủ ghi bàn.
A. \(0,14\)
B. \(0,38\)
C. \(0,24\)
D. \(0,62\)
Lời giải: Gọi $A$ là trở nên cố cầu thủ loại nhất ghi được bàn thắng.
Ta với \(P\left( A \right) = 0,8\) và \(P(\overline A ) = 0,2\)
Gọi $B$ là trở nên cố cầu thủ loại nhất ghi được bàn thắng.
Ta với \(P\left( B \right) = 0,7\) và \(P(\overline B) = 0,3\)
Ta xét nhì trở nên cố xung xung khắc sau:
\(A\overline B\) “Chỉ với cầu thủ loại nhất thực hiện bàn”.
Ta có:
\(P\left( {A\overline B} \right) = P\left( A \right).P\left( {\overline B} \right) \) \(= 0,8.0,3 = 0,24\)
\(B\bar A\) “ Chỉ với cầu thủ loại nhì thực hiện bàn” .
Ta có:
$P\left( {B\overline A} \right) = P\left( B \right).P\left( {\overline A} \right) $ $= 0,7.0,2 = 0,14$
Gọi $C$ là trở nên cố chỉ mất $1$ cầu thủ ghi bàn.
Ta với \(P(C) = 0,24 + 0,14 = 0,38\)
Chọn đáp án B.
